
Feed-in tariff: A policy tool encouraging deployment of renewable electricity technologies
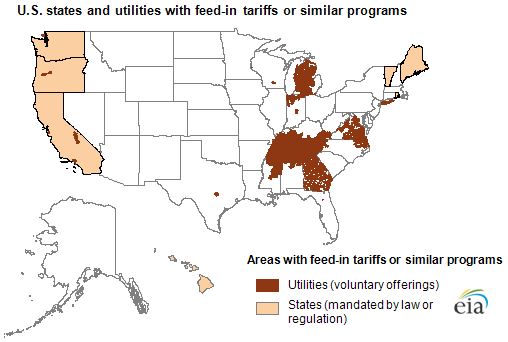
Recent developments in Virginia put a spotlight on feed-in tariffs (FITs), which are a policy mechanism used to encourage deployment of renewable electricity technologies. FITs are used to a limited extent around the United States, but they are more common internationally. A FIT program typically guarantees that customers who own a FIT-eligible renewable electricity generation facility, such as a roof-top solar photovoltaic system, will receive a set price from their utility for all of the electricity they generate and provide to the grid.
Historically, FITs have been associated with a German model in which the government mandates that utilities enter into long-term contracts with generators at specified rates, typically well above the retail price of electricity. In the United States, where FITs are comparatively new, FITs or similarly structured programs are mandated to varying degrees in a limited number of states. However, a different model has also emerged in which utilities independently establish a utility-level FIT, either voluntarily or in response to state or local government mandates.
In a recent example, Dominion Virginia Power's voluntary FIT for residential and commercial solar photovoltaic (PV) generators was approved by the Virginia State Corporation Commission in March 2013. Participants will receive 15 cents/kilowatthour (kWh) for a contract term of five years for all PV-generated electricity provided to the grid, and will continue to pay the retail rate for all electricity that they consume. Virginia's average 2012 retail electricity price was 10.5 cents/kWh for residential customers and 7.8 cents/kWh for commercial customers.
Comparison with other policy tools
Other types of policies encouraging development of new renewable capacity that are more commonly used in the United States include:
- Rebates for purchasing renewable generation equipment
- Renewable portfolio standards (RPS)
- Net metering
- Tax incentives (production- or investment-based) such as the federal wind production tax credit
A FIT is a performance-based incentive rather than an investment-based incentive, and in that respect is more similar to production tax credits and the renewable energy credits of an RPS market than to investment tax credits or other investment subsidies. In the United States, FITs are typically used in combination with one or more of these other incentives.
FITs are most similar to the federal Qualifying Facility (QF) incentives available in the United States since the late 1970s, although the QF contracts were limited to paying avoided cost rates based on the utility's cost-of-generation rather than the above-utility-cost rates typical of a FIT. FIT programs are also similar to net metering programs but differ significantly in one key aspect: the power generated by a utility customer's system is compensated at the rate set by the FIT rather than the retail electricity rate. This generation is treated independently from the customer's own electricity use, which is billed at the utility's regular retail rates. In a net metering program, a utility customer is effectively paid the retail rate for any generation that is fed back into the grid.
Variations on feed-in tariff policies
In general, feed-in tariff rates that lead to significant additional renewable energy investment are set above the retail cost of electricity. The premium level may depend on the underlying program motivation and goals: FIT programs associated with more ambitious goals (e.g., an explicit capacity target, or a certain level of renewable energy credits to meet an RPS obligation, or to support a domestic renewable energy industry) may need to set the rate well in excess of the existing retail price. In a recent example, in 2012 Japan implemented a new FIT with particularly high PV tariff rates (more than 40 cents/kWh) as part of its post-Fukushima policy.
However, without additional controls, generous FIT levels can lead to more investment than intended. One illustration is the Spanish experience, in which the government significantly reduced the tariff a year after its start, and suspended the FIT altogether in 2012, to contain costs to the government and other utility customers.
Feed-in tariffs vary widely in execution. EIA is now publishing a new table on the variety of feed-in tariffs used in the United States. Typically, feed-in tariffs will specify:
Eligible technologies—FITs in the United States generally include solar PV, but may include other renewable technologies. Other countries' FITs, particularly the German and Danish programs where the policy was tested and developed, initially focused on supporting wind. In U.S. states with an RPS, the FIT-eligible technologies generally overlap or coincide with RPS-eligible technologies: for example, the FIT set by the Los Angeles Department of Water and Power applies to all technologies eligible for the California RPS. The FIT set by Florida's Gainesville Regional Utilities, the first U.S. municipal utility to institute a FIT, applies only to solar PV generators.
Rate and contract terms—Excluding some experimental programs, most U.S. contracts are long term (10-20 years). This assures project owners of a stable long term revenue stream. Utilities often set rates that depend on project size (smaller projects tend to receive higher rates) and technology (solar PV tends to receive higher rates than other technologies). Rates can also depend on the overall program goal or size limits (e.g., tariffs that decrease as capacity approaches the program ceiling), and utilities or states may revise their tariffs in cases of over- or under-subscription. The City of Palo Alto Utilities CLEAN program initially set its uniform tariff rate for PV based on the utility's avoided cost of providing electricity; however, after low customer interest as a result of the minimal premium, the utility has since raised the tariff rate by more than 15% while reducing the program size.
System size and sector restrictions—Most U.S. FIT programs have a maximum size for individual projects and may limit participation to certain sectors, like residential customers. The new Dominion Virginia Power Solar Purchase Program, for example, applies only to residential systems up to 20 kilowatts (kW) and commercial systems up to 50 kW in size, while Hawaii's FIT, which applies to all of Hawaii's investor-owned utilities, has a maximum system size ranging from 2,700 kW to 5,000 kW, depending on the island.
Program size limitations—Most U.S. programs designate a cumulative ceiling, set either annually or at the program level, capping the amount of capacity that can take advantage of the tariff. This is an important cost containment mechanism for FIT programs.
Tags: electricity, generation, policy, renewables, solar