|
Download Data (XLS File) |
|
||||||||
 |
||||||||
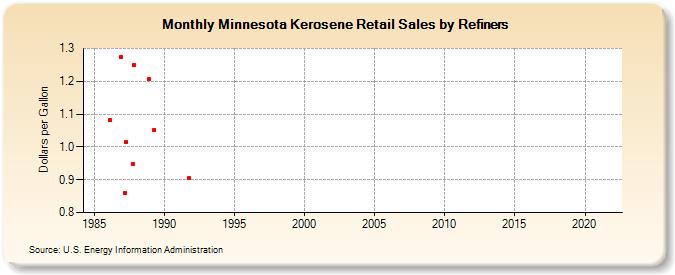
| Minnesota Kerosene Retail Sales by Refiners (Dollars per Gallon) | ||||||||
| Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1984 | - | W | W | W | ||||||||
| 1985 | W | W | W | W | - | - | - | W | W | W | W | W |
| 1986 | W | 1.081 | W | W | W | W | W | W | W | W | 1.273 | W |
| 1987 | W | W | 0.859 | 1.015 | W | W | W | W | W | 0.949 | 1.250 | W |
| 1988 | W | W | W | W | W | W | W | W | W | W | 1.206 | W |
| 1989 | W | W | W | 1.051 | W | - | W | W | W | W | W | W |
| 1990 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1991 | W | W | W | W | W | W | W | W | W | 0.904 | W | W |
| 1992 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1993 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1994 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1995 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1996 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1997 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1998 | W | W | W | W | W | W | W | W | W | W | W | W |
| 1999 | W | W | W | W | W | W | W | W | W | W | W | W |
| 2000 | W | - | W | - | W | W | W | W | W | W | W | W |
| 2001 | W | - | W | - | - | - | - | - | - | - | - | - |
| 2002 | - | - | - | - | - | - | - | - | - | - | - | W |
| 2003 | W | W | - | - | W | W | - | - | - | W | W | W |
| 2004 | W | - | W | W | W | W | - | W | W | - | W | W |
| 2005 | W | W | W | W | W | - | W | - | W | W | - | W |
| 2006 | W | W | W | W | - | - | W | - | W | - | W | W |
| 2007 | - | W | - | - | - | - | - | - | - | - | W | W |
| 2008 | W | W | W | - | - | - | - | - | - | - | W | W |
| 2009 | W | W | W | - | - | - | - | - | - | - | - | W |
| 2010 | W | W | - | - | - | - | - | - | - | - | W | - |
| 2011 | - | - | - | - | - | - | - | - | - | - | W | W |
| 2012 | W | W | - | - | - | - | - | - | - | W | W | W |
| 2013 | W | W | W | W | - | - | - | - | - | W | W | W |
| 2014 | W | W | W | W | - | - | - | - | - | - | W | W |
| 2015 | W | W | W | - | - | - | - | - | - | - | W | W |
| 2016 | W | W | W | - | W | NA | W | W | W | W | W | W |
| 2017 | W | W | W | W | W | W | W | W | W | W | W | W |
| 2018 | W | W | W | W | W | W | W | W | W | W | W | W |
| 2019 | W | W | W | W | W | W | W | W | W | W | W | W |
| 2020 | W | W | W | W | W | W | W | W | W | W | W | W |
| 2021 | W | W | W | W | W | W | W | W | W | W | W | W |
| 2022 | W | W | W | |||||||||
| - = No Data Reported; -- = Not Applicable; NA = Not Available; W = Withheld to avoid disclosure of individual company data. |
| Release Date: 6/1/2022 |
| Next Release Date: TBD |